Approximate floating-point multiplication

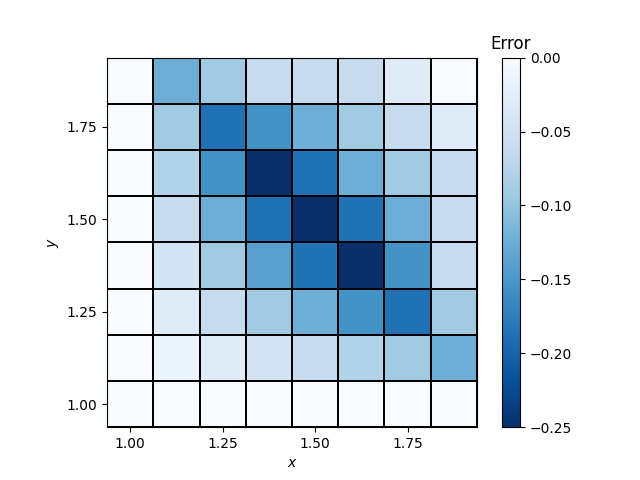
This example compares an approximate floating-point multiplication to the mathematically correct result. The approximation is based on Mitchell’s logarithm approximation and the reference is the unquantized result.

(Example inspired from T. Lindberg and O. Gustafsson, “Exact Eight-Bit Floating-Point Multiplication Using Integer Arithmetic”, in Proc. Asilomar Conf. Signals Syst. Comput., 2025.)

import matplotlib.pyplot as plt
from matplotlib import ticker

import apytypes as apy

EXP_BITS, MAN_BITS = (4, 3)

input_values = apy.fullrange(1, 2, exp_bits=EXP_BITS, man_bits=MAN_BITS)

xx, yy = apy.meshgrid(input_values, input_values)

# Calculate the reference using a format wide enough to capture the exact result
ref = xx.cast(EXP_BITS, 2 * MAN_BITS) * yy


def approx_mul(x, y):
    return apy.APyFloat.from_bits(
        x.to_bits() + y.to_bits() - (x.bias << x.man_bits), EXP_BITS, MAN_BITS
    )


result = apy.zeros_like(ref, exp_bits=EXP_BITS, man_bits=MAN_BITS)
for xi, x in enumerate(input_values):
    for yi, y in enumerate(input_values):
        result[xi, yi] = approx_mul(x, y)

error = result - ref

Plot the results

fig, ax = plt.subplots()

ax.set_xlabel(r"$x$")
ax.set_ylabel(r"$y$")
ax.set_aspect("equal")

ax.xaxis.set_major_locator(ticker.MultipleLocator(2 * 2**-MAN_BITS))
ax.yaxis.set_major_locator(ticker.MultipleLocator(2 * 2**-MAN_BITS))

pcol = ax.pcolormesh(
    xx.to_numpy(), yy.to_numpy(), error.to_numpy(), ec="k", lw=0.1, cmap="Blues_r"
)
cbar = fig.colorbar(pcol)
cbar.ax.set_title("Error")

plt.show()