Fixed-point vector rotation

This illustrates the effect of performing a vector rotation using different number of fractional bits and different quantization schemes.

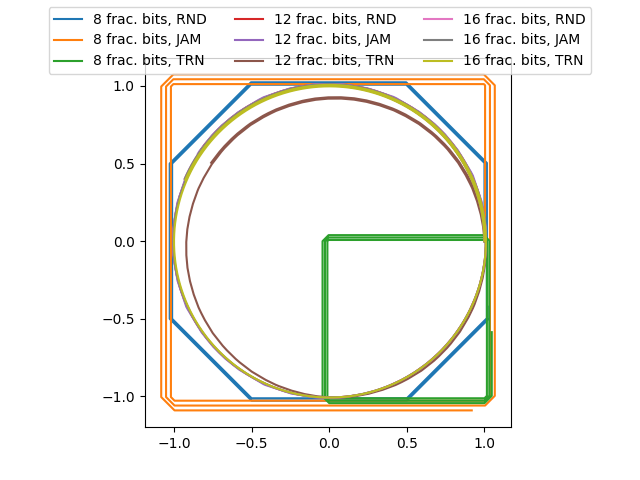
8 fractional bits. Gain: 1.0000076293654276. Angle: 0.0039062301319669718.
12 fractional bits. Gain: 1.0000042915252152. Angle: 0.0029296791181399936.
16 fractional bits. Gain: 1.000004517952019. Angle: 0.003005972391421174.

import apytypes as apy
import math
import matplotlib.pyplot as plt
import numpy as np

angle = 0.003


def print_rotation_properties(angle, frac_bits):
    cosa = math.cos(angle)
    sina = math.sin(angle)
    rotation_matrix = apy.fx([[cosa, -sina], [sina, cosa]], 2, frac_bits)
    rm = rotation_matrix.to_numpy()
    print(
        f"{frac_bits} fractional bits. Gain: {np.hypot(*rm[0, :])}. Angle: {np.arctan2(*rm[1, :])}."
    )


def rotate(angle, frac_bits, iterations, quantization):
    results = apy.zeros((iterations + 1, 2), int_bits=2, frac_bits=frac_bits)
    cosa = math.cos(angle)
    sina = math.sin(angle)
    rotation_matrix = apy.fx([[cosa, -sina], [sina, cosa]], 2, frac_bits)
    current_value = apy.fx([1, 0], 2, frac_bits)

    results[0, :] = current_value.T
    for i in range(iterations):
        tmp_res = rotation_matrix @ current_value
        current_value = tmp_res.cast(2, frac_bits, quantization)
        results[i + 1, :] = current_value.T

    return results


fig, ax = plt.subplots()

for frac_bits in (8, 12, 16):
    print_rotation_properties(angle, frac_bits)
    for quantization in (
        "RND",
        "JAM",
        "TRN",
    ):
        results = rotate(
            angle, frac_bits, 3000, eval(f"apy.QuantizationMode.{quantization}")
        )
        ax.plot(
            results[:, 0],
            results[:, 1],
            label=f"{frac_bits} frac. bits, {quantization}",
        )

ax.set_aspect("equal")
fig.legend(ncols=3, loc="upper center")
plt.show()