Quantization and overflow handling

Quantization modes

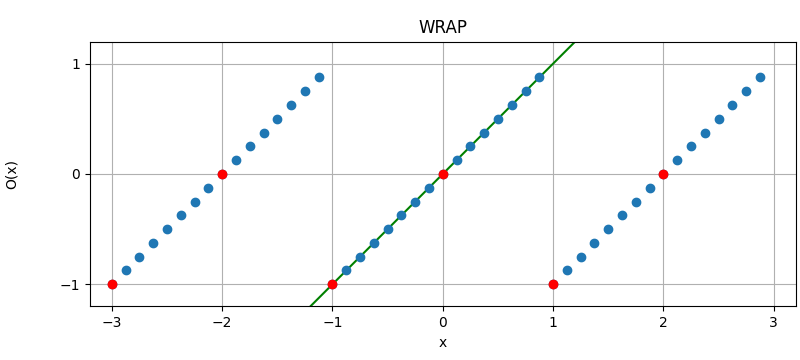
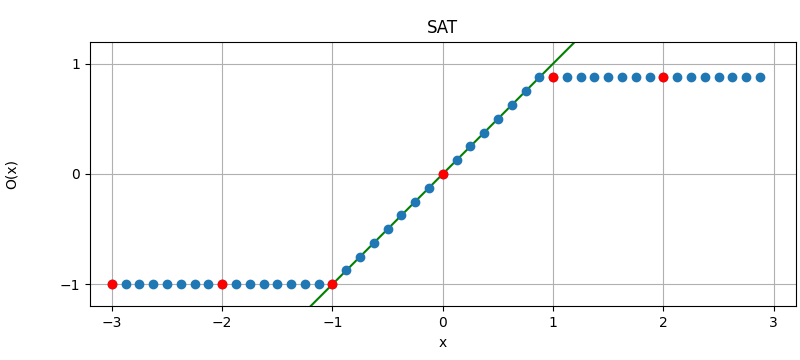
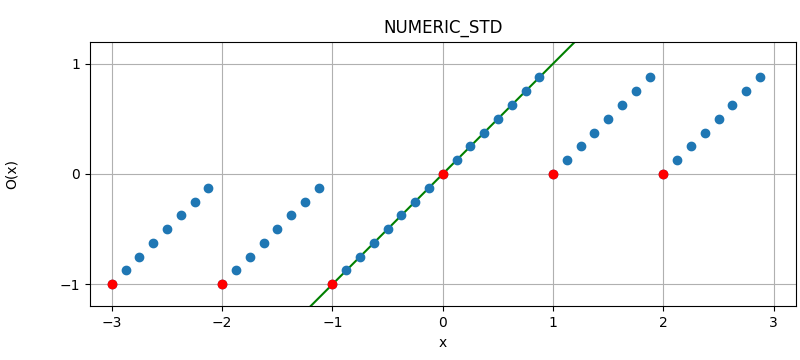
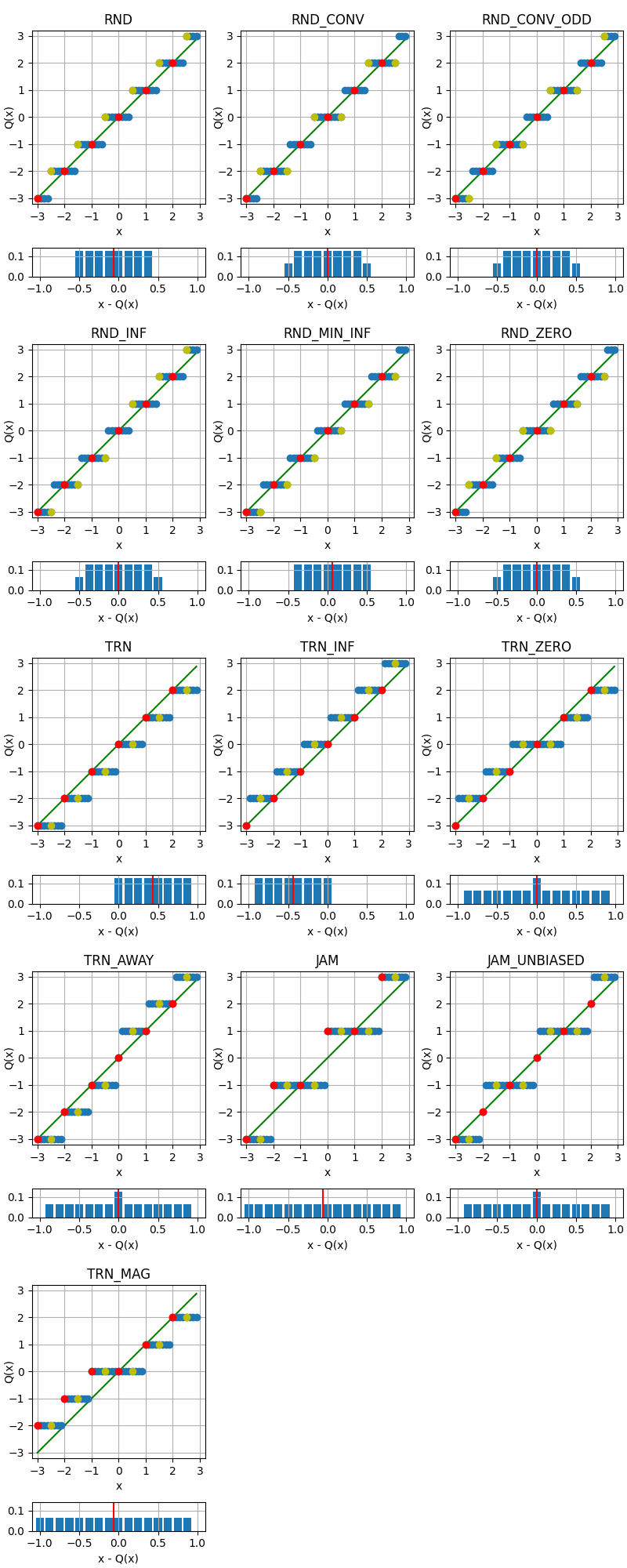
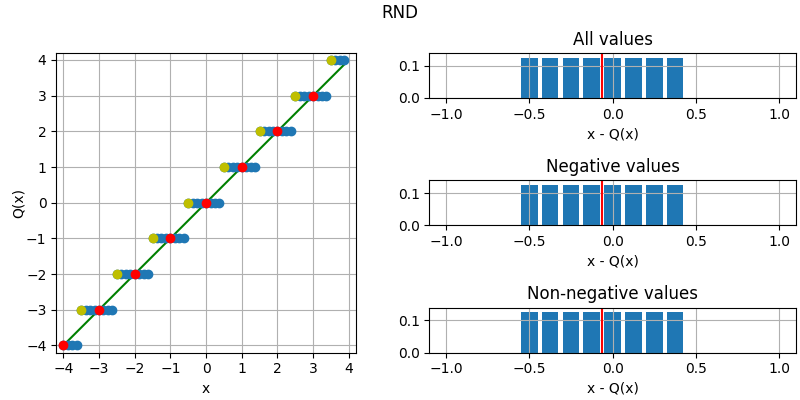
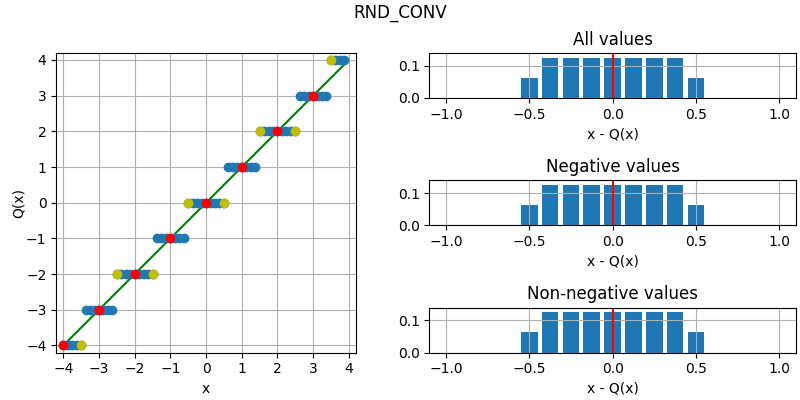
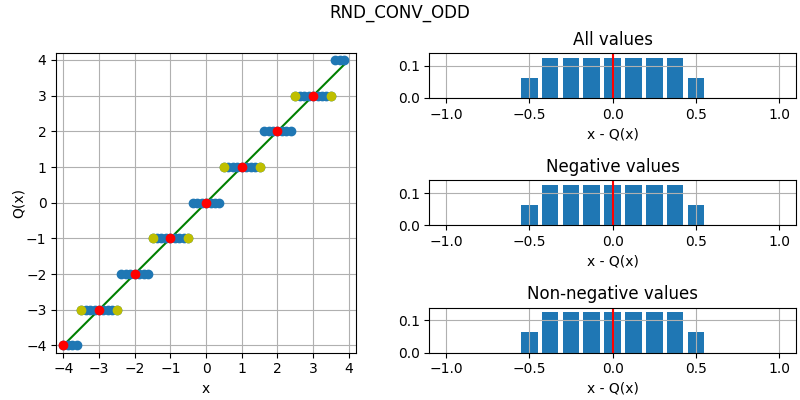
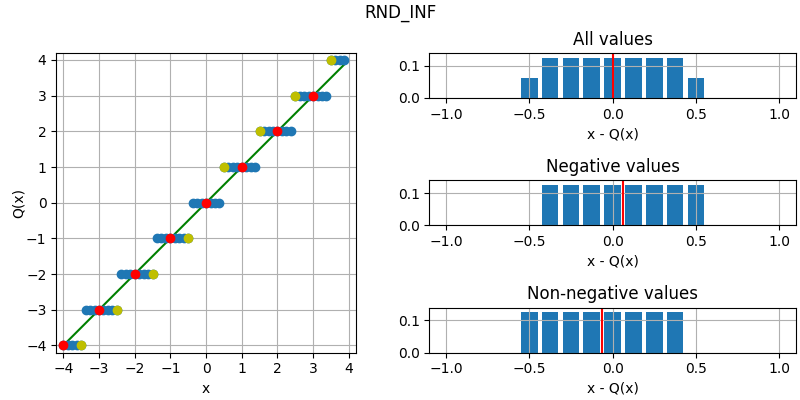
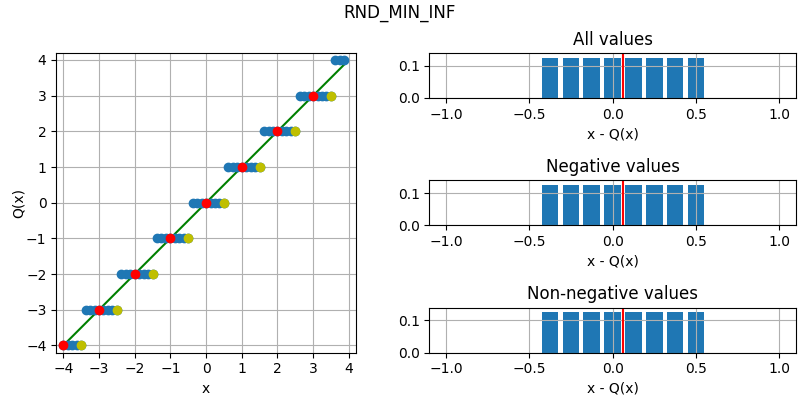
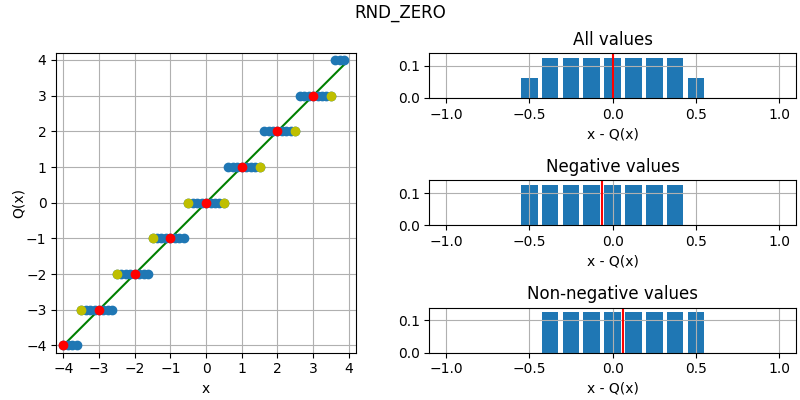
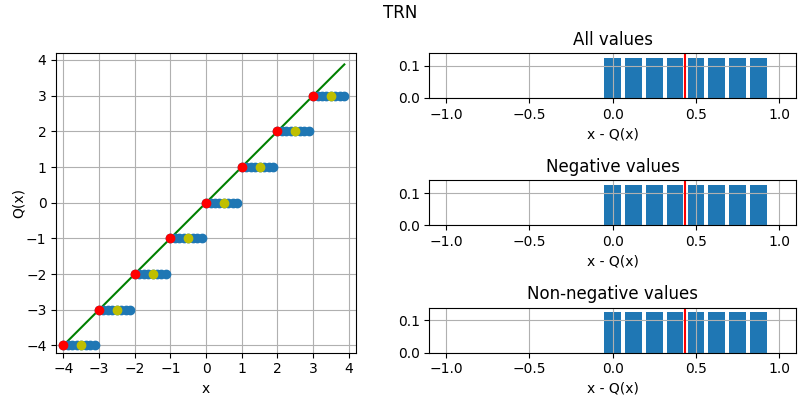
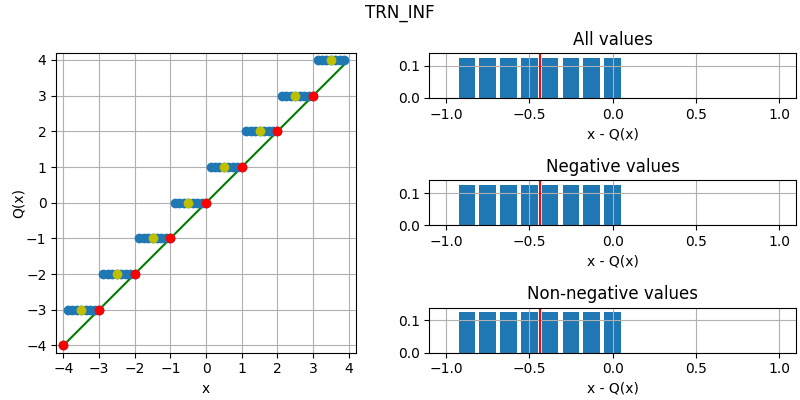
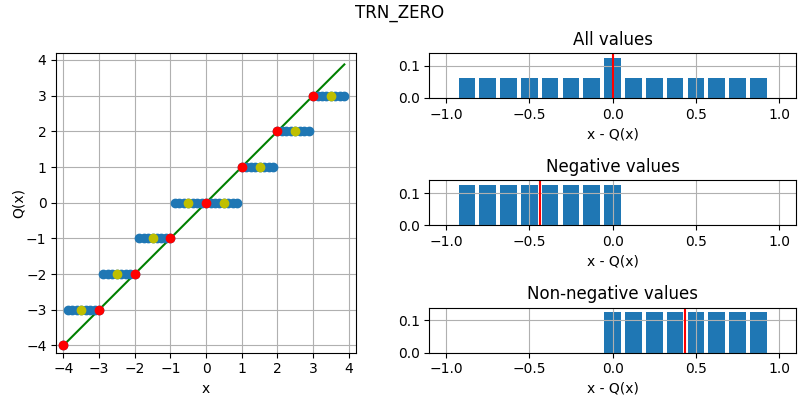
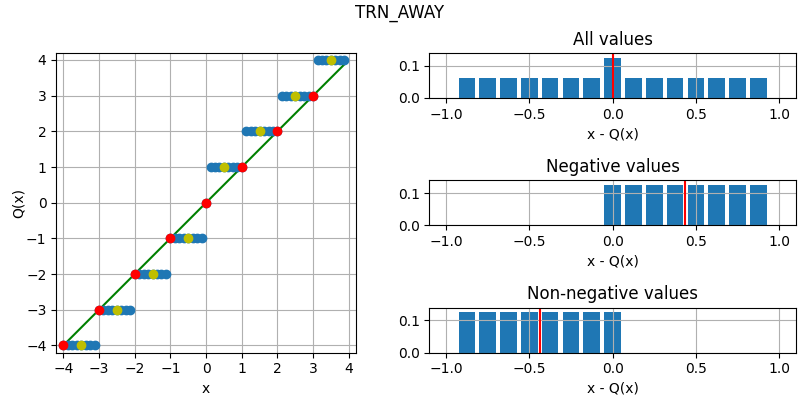
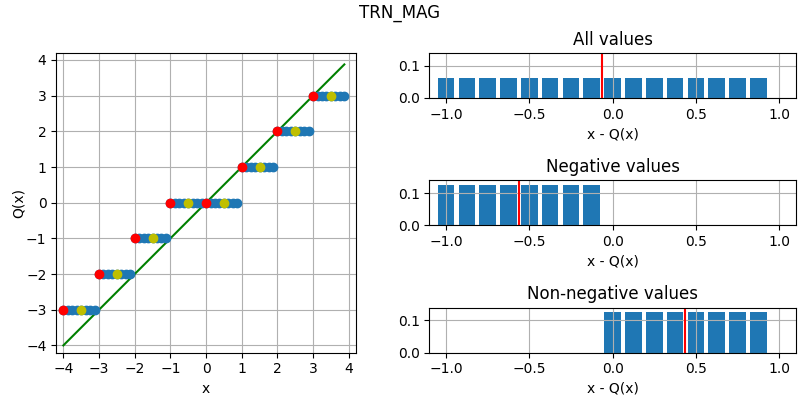
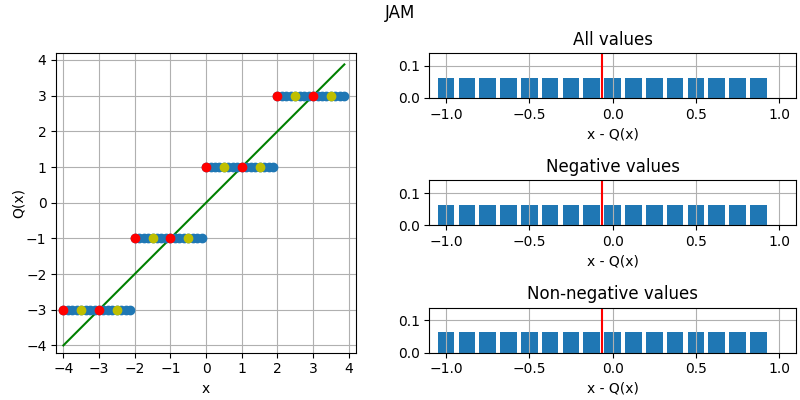
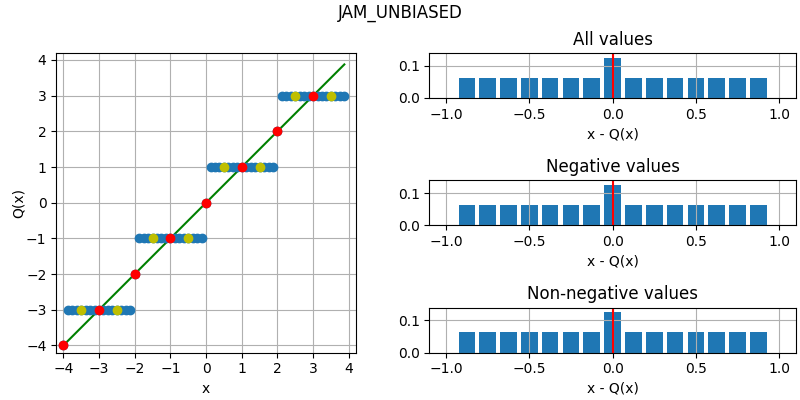
The following figure illustrates the effect of the different quantization modes on quantizing a fixed-point number with three fractional bits to none. The dots corresponds to different values, where the red dots correspond to numbers that were initially an integer and yellow dots to numbers that are exactly between two integers (ties). Below each plot is an error distribution histogram, where the red line indicates the bias (average error) of the quantization. Note that the bias will converge towards zero the more bits are quantized away (except for QuantizationMode.TRN, which will converge towards a half).

class apytypes.QuantizationMode(value)

RND = 5

Round to nearest, ties toward positive infinity.

RND_CONV = 9

Round to nearest, ties to even.

RND_CONV_ODD = 10

Round to nearest, ties to odd.

RND_INF = 7

Round to nearest, ties away from zero.

RND_MIN_INF = 8

Round to nearest, ties toward negative infinity.

RND_ZERO = 6

Round to nearest, ties towards zero.

TRN = 0

Round towards negative infinity (truncation).

Implementation: remove additional bits.

TRN_INF = 1

Round towards positive infinity.

TRN_ZERO = 2

Round towards zero (unbiased magnitude truncation).

TRN_AWAY = 3

Round away from zero.

TRN_MAG = 4

Fixed-point magnitude truncation (add sign-bit).

JAM = 11

Jamming/von Neumann rounding.

JAM_UNBIASED = 12

Unbiased jamming/von Neumann rounding.

Aliases

TO_NEG = 0

Fixed-point truncation. Round towards negative infinity. Alias for TRN.

TO_POS = 1

Round towards positive infinity. Alias for TRN_INF.

TO_ZERO = 2

Unbiased magnitude truncation. Round towards zero. Alias for TRN_ZERO.

TO_AWAY = 3

Round away from zero. Alias for TRN_AWAY.

TIES_POS = 5

Fixed-point rounding. Round to nearest, ties toward positive infinity. Alias for RND.

TIES_EVEN = 9

Unbiased fixed-point rounding. Round to nearest, ties to even. Alias for RND_CONV.

TIES_ODD = 10

Alternate unbiased fixed-point rounding. Round to nearest, ties to odd. Alias for RND_CONV_ODD.

TIES_AWAY = 7

Round to nearest, ties away from zero. Alias for RND_INF.

TIES_NEG = 8

Round to nearest, ties toward negative infinity. Alias for RND_MIN_INF.

TIES_ZERO = 6

Round to nearest, ties toward zero. Alias for RND_ZERO.

Utility functions

apytypes.get_float_quantization_mode() → QuantizationMode

Get current quantization context.

Returns:

QuantizationMode

See also

set_float_quantization_mode

apytypes.set_float_quantization_mode(mode: QuantizationMode) → None

Set current quantization context.

Parameters:

modeQuantizationMode

The quantization mode to use.

See also

get_float_quantization_mode

apytypes.get_float_quantization_seed() → int

Set current quantization seed.

The quantization seed is used for stochastic quantization.

Returns:

int

See also

set_float_quantization_seed

apytypes.set_float_quantization_seed(seed: int) → None

Set current quantization seed.

The quantization seed is used for stochastic quantization.

Parameters:

seedint

The quantization seed to use.

See also

get_float_quantization_seed

Sign of zero for floating-point

For multiplication and division the sign is always the XOR of the operands’ signs, but for addition and subtraction the sign depends on the quantization mode. Below is a table showing what the sign of zero will be in different cases. Using this table one can derive the sign for subtraction as well.

Sign of zero in floating-point addition

\(x + y\)	TO_NEG	Other modes
\((+0) + (+0)\)	\(+0\)	\(+0\)
\((+0) + (-0)\)	\(-0\)	\(+0\)
\((-0) + (+0)\)	\(-0\)	\(+0\)
\((-0) + (-0)\)	\(-0\)	\(-0\)
\(x + y, x = -y\)	\(-0\)	\(+0\)

Overflow modes

class apytypes.OverflowMode(value)

WRAP = 0

Two’s complement wrapping.

SAT = 1

Two’s complement saturation.

NUMERIC_STD = 2

Keep sign bit and remove intermediate bits.

As resize for signed in ieee.numeric_std.