Reciprocal lookup table

In this example a lookup table for floating-point reciprocals is designed, assuming that each bit is implemented using an N-ínput LUT, suitable for FPGA, and single-precision floating-point representation.

import apytypes as apy
import numpy as np
import matplotlib.pyplot as plt

N = 6
WL = 9

step = apy.APyFixed(1, 3, N)
r = apy.arange(1, 2 + 2**-6, step=step)

table = apy.zeros((2**6,), 1, WL)
float_table = []
for i in range(2**6):
    start = float(r[i])
    stop = float(r[i + 1])

    meanreciprocal = (1 / start + 1 / stop) / 2
    float_table.append(meanreciprocal)
    table[i] = apy.fx(meanreciprocal, 1, WL)

Print the resulting table

fstring = f"{{:{WL}b}}"
for b in table.to_bits():
    print(fstring.format(b))

111111100
111110100
111101101
111100101
111011110
111011000
111010001
111001010
111000100
110111110
110111000
110110010
110101100
110100111
110100001
110011100
110010111
110010010
110001101
110001000
110000100
101111111
101111011
101110111
101110010
101101110
101101010
101100110
101100010
101011110
101011011
101010111
101010100
101010000
101001101
101001001
101000110
101000011
101000000
100111101
100111010
100110111
100110100
100110001
100101110
100101011
100101001
100100110
100100011
100100001
100011110
100011100
100011001
100010111
100010101
100010010
100010000
100001110
100001011
100001001
100000111
100000101
100000011
100000001

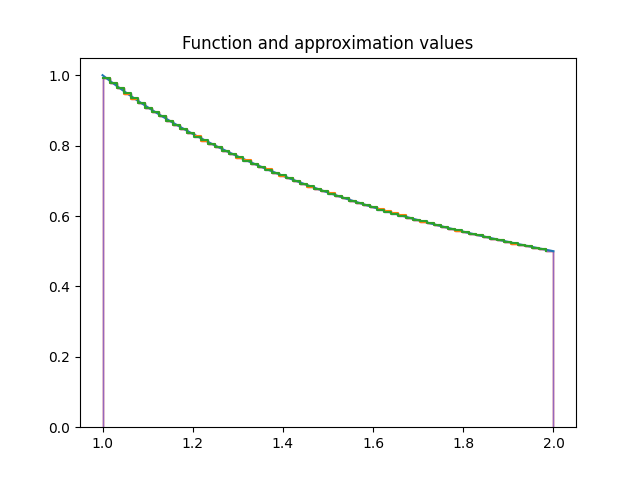
Plot the approximation, with and without fixed-point values

f = np.linspace(1, 2, 10000)
fig, ax = plt.subplots()

ax.plot(f, 1 / f)
ax.step(r[:-1], table, where="post")
ax.step(r[:-1], float_table, where="post")
ax.stairs(table.to_numpy(), r.to_numpy())
ax.stairs(float_table, r.to_numpy())
ax.set_title("Function and approximation values")
plt.show()

Compute seed error and after one Newton-Raphson iteration

points = 10000


def eval_seed(x, table):
    table_row = x.man >> (23 - N)  # N most significant bits of x
    new_exp = 253 - x.exp
    new_man = (table[table_row].to_bits() & ((1 << (WL - 1)) - 1)) << (23 - WL + 1)
    res = apy.APyFloat(x.sign, new_exp, new_man, 8, 23)
    return res


fval = np.linspace(1, 2, points)
seed_table = apy.zeros((points,), exp_bits=8, man_bits=23)
nr_table = apy.zeros((points,), exp_bits=8, man_bits=23)

for i in range(points):
    x = apy.fp(fval[i], 8, 23)
    seed = eval_seed(x, table)
    seed_table[i] = seed
    # Perform one Newton-Raphson iteration
    refined = seed + seed * (1 - seed * x)
    nr_table[i] = refined

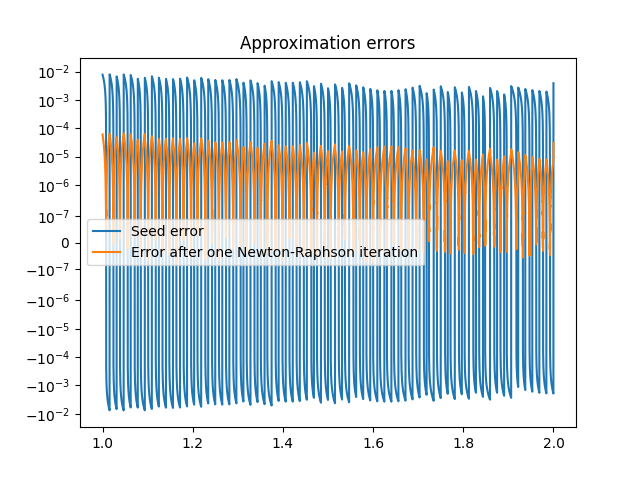
Plot resulting errors

fig, ax = plt.subplots()
ax.plot(fval, 1 / fval - seed_table, label="Seed error")
ax.plot(fval, 1 / fval - nr_table, label="Error after one Newton-Raphson iteration")
ax.set_yscale("symlog", linthresh=2**-23)
ax.legend()
ax.set_title("Approximation errors")
plt.show()